图
定义:
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
图的描述
//点,包含值,入度,出度,邻界点和边
public class Node{
public int value;
public int in;
public int out;
public ArrayList<Node> nexts;
public ArrayList<Node> edges;
public Node(int val){
this.value = val;
this.in = 0;
this.out = 0;
this.nexts = new ArrayList<>();
this.edges = new ArrayList<>();
}
}
//边,包含尾,头和权重
public class Edge{
public Node from;
public Node to;
public int weight;
public Edge(Node n1,Node n2,int w){
this.from = n1;
this.to = n2;
this.weight = w;
}
}
public class Graph{
public HashMap<Integer,Node> nodes;
public HashSet<Edge> edges;
public Graph(){
this.nodes = new HashMap<>();
this.edges = new HashSet<>();
}
}
// matrix 所有的边
// N*3 的矩阵
// [weight, from节点上面的值,to节点上面的值]
//
// [ 5 , 0 , 7]
// [ 3 , 0, 1]
//构造图
public static Graph createGraph(int[][] matrix){
Graph graph = new Graph();
for(int i = 0;i < matrix.length;i++){
int weight = matrix[i][0];
int from = matrix[i][1];
int to = matrix[i][2];
if(!graph.nodes.containsKey(from)){
graph.nodes.put(from,new Node(from));
}
if(!graph.nodes.containsKey(to)){
graph.nodes.put(to,new Node(to));
}
Node fromN = graph.nodes.get(from);
Node toN = graph.nodes.get(to);
Edge edge = new Edge(fromN,toN,weight);
graph.edges.add(edge);
toN.in++;
fromN.nexts.add(toN);
fromN.out++;
fromN.edges.add(edge);
}
return graph;
}
两种遍历方式
宽度优先遍历
1.和二叉树类似,声明一个队列和Set,Set记录顶点Node,进去过的不在进入队列
public static void bfs(Node start){
if(start == null){
return;
}
Queue<Node> queue = new LinkedList<>();
Set<Node> set = new HashSet<>();
queue.add(start);
set.add(start);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.value);
for(Node next : cur.nexts){
if(!set.contains(next)){
queue.add(next);
set.add(next);
}
}
}
}
深度优先遍历
1.声明一个堆和Set,每次放入都将他和上一个顶点放入stack中,然后退出当前顶点的nexts的for循环
public static void dfs(Node start){
if(start == null){
return;
}
Stack<Node> stack = new Stack<>();
Set<Node> set = new HashSet<>();
stack.add(start);
System.out.println(start.value);
set.add(start);
while(!stack.isEmpty()){
Node cur = stack.pop();
for(Node next:cur.nexts){
if(!set.contains(next)){
stack.add(cur);
stack.add(next);
set.add(next);
System.out.println(next.value);
break;
}
}
}
}
拓扑排序
定义
-
在图中找出所有入度为0的点输出
-
把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始
-
图的所有点都被删除后,依次输出的顺序就是拓扑排序
要求
- 要求:有向图且其中没有环
- 应用:事件安排,编译顺序
思路:
//1.设置queue zeroInQueue ,把in = 0放入队列,设置List ans
//2.当node进入inQueue,则他对应的邻居 inNode--,因此设定一个结构Map<Node,Integer>inMap,记录每个节点对应的入度
//3.先找出入度=0的节点放入0入度队列
//4。从0队列中弹出节点,当前节点必定是入度为0的节点,放入ans中。
//5.通过inMap,可以消除当前这个节点对其它节点的影响,当前节点入度=0,放入ans中,则表明该节点已完成,则其他依赖此节点的节点的in--
//6.对queue重复循环,完成上面的ans,返回
public static List<Node> sortedTopology(Graph graph) {
Queue queue = new LinkedList<>();
List<Node> ans = new ArrayList<>();
HashMap<Node,Integer> inMap = new HashMap<>();
for(Node cur:graph.nodes){
inMap.put(cur,cur.in);
if(cur.in == 0){
queue.add(cur);
}
}
while(!queue.isEmpty()){
Node cur = queue.poll();
ans.add(cur);
for(Node next : cur.nexts){
inMap.put(next,inMap.get(next)-1);
if(inMap.get(next)==0){
queue.add(next);
}
}
}
return ans;
}
Kruskal算法
//最小生成树算法之Kruskal
//1.总是从权值最小的边开始考虑,依次考察权值依次变大的边
//2.当前的边要么进入最小生成树的集合,要么丢弃
//3.如果当前的边进入最小生成树的集合中不会形成环,就要当前边
//4.如果当前的边进入最小生成树的集合中会形成环,就不要当前边
//5.考察完所有边之后,最小生成树的集合也得到了
//贪心,对所有edge做个小顶堆(权重)
//对边的from和to做个判断,是否已经成环,可以用UnionFind,并查集实现
//成环的,舍弃这条边,继续下一条边,直到当前点都在一个集合中
public static Set<Edge> kruskalMST(Graph graph){
UnionFind uf = new UnionFind(graph.nodes);
PriorityQueue<Edge> queue = new PriorityQueue<>(new Comporator<Edge>(){
@Override
public int compare(Edge o1,Edge o2){
return o1.weight <= o2.weight ? -1 : 1;
}
});
for(Edge edge : graph.edges){
queue.add(edge);
}
Set<Edge> ans = new HashSet<>();
while(uf.sets() > 1){
Edge cur = queue.poll();
Node from = cur.from;
Node to = cur.to;
if(!uf.isSameSet(from,to)){
ans.add(cur);
uf.union(from,to);
}
}
return ans;
}
public static class UnionFind{
private HashMap<Node,Node> parents;
private HashMap<Node,Integer> sizeMap;
public UnionFind(HashMap<Integer,Node> nodes){
parents = new HashMap<>();
sizeMap = new HashMap<>();
for(Node node : node.value()){
parents.put(node,node);
sizeMap.put(node,1);
}
}
private Node find(Node n){
Stack<Node> stack = new Stack<>();
while(n != parents.get(n)){
stack.push(n);
n = parents.get(n);
}
while(!stack.isEmpty()){
parents.put(stack.pop(),n);
}
return n;
}
public void union(Node n1,Node n2){
Node f1 = find(n1);
Node f2 = find(n2);
if(f1 != f2){
Node big = sizeMap.get(f1) >= sizeMap.get(f2) ? f1:f2;
Node small = big == f1 ? f2 f2 : f1;
parents.put(small,big);
sizeMap.put(big,sizeMap.get(big) + sizeMap.get(small));
sizeMap.remove(small);
}
}
public boolean isSameSet(Node n1,Node n2){
return find(n1) == find(n2);
}
public int sets(){
return sizeMap.get();
}
}
Prim算法
//最小生成树算法之Prim
//1.可以从任意节点出发来寻找最小生成树
//2.某个点加入到被选取的点后中后,解锁这个点出发的所有的新的边
//3.在所有解锁的边中选最小的边,然后看看这个边会不会形成环
//4.如果会,不要当前边,继续考察剩下解锁的边中最小的边,重复3
//5.如果不会,要当前边,将该边的指向点加入到被选取的点中,重复2
//6.当所有点都被选取,最小生成树就得到了
//1,弄一个堆,存放edge,Set存放点,判断当前点是否都加入进去了
//2.for循环(防止树的出现),解锁当前循环的第一个点,然后这个点解锁新的边,存放在edge中
//3.从这个edge解锁新的点,如果这个点不在Set里,这个edge存放在ans,然后对下一个点继续上述操作
public static Set<Edge> primMST(Graph graph) {
PriorityQueue<Edge> queue = new PriorityQueue<new Comparator<Edge>(){
@Override
public int compare(Edge o1,Edge o2){
return o1.weight <= o2.weight ? -1 : 1;
}
});
Set<Node> set = new HashSet<>();
Set<Edge> ans = new HashSet<>();
for(Node node:graph.nodes.values()){
if(!set.contains(node)){
set.add(node);
for(Edge edge : node.edges){
queue.add(edge);
}
while(!queue.isEmpty()){
Edge cur = queue.poll();
Node to = queue.poll().to;
if(!set.contains(to)){
set.add(to);
ans.add(cur);
for(Edge edge : to.edges){
queue.add(edge);
}
}
}
}
}
return ans;
}
// 请保证graph是连通图
// graph[i][j]表示点i到点j的距离,如果是系统最大值代表无路
// 返回值是最小连通图的路径之和
//思路:
//1.graph.length是当前的节点数,用len表示
//2.distance[]记录当前到的节点的最小权重
//3.visit[]记录当前节点的访问情况
//4.for循环,每次找出当前最小权重的点,然后更新这个点更新后的新的权重的边
public static int prim(int[][] grahp){
int len = graph.length;
int[] dis = new int[len];
boolean[] visit = new boolean[len];
visit[0] = true;
for(int i = 0;i<len ; i++){
dis[i] = graph[0][i];
}
int sum = 0;
for(int i = 0;i < len;i++){
int minDis = Integer.MAX_VALUE;
int minIndex = -1;
for(int j = 0;j < len;j++){
if(!visit[j] && minDis > dis[j]){
minDis = dis[j];
minIndex = j;
}
}
if(minIndex == -1){
retur sum;
}
sum += minDis;
visit[minIndex] = true;
for(int j = 0;j<len;j++){
dis[j] = Math.min(dis[j],graph[minIndex][j]);
}
}
return sum;
}
Dijkstra算法
//单元到每个点的最小路径
//选择一个点作为起始点,然后from这个点出发,
//1.从from这个点中解锁所有的边,用hashMap记录当前从from到每个点的最小距离
//2.选择除了from以外的最小距离的点,然后解锁新的边和距离,直到所有距离都更新完
//3.用Set记录当前以选择的点
public static HashMap<Node,Integer> dijkstra1(Node from){
HashMap<Node,Integer> nodeDis = new HashMap<>();
nodeDis.put(from,0);
Set<Node> set = new HashSet<>();
Node minNode = selectMinNode(nodeDis,set);
while(minNode != null){
int dis = nodeDis.get(minNode);
for(Edge edge : minNode.edges){
if(!nodeDis.containsKey(edge.to)){
nodeDis.put(edge.to,edge.weight + dis);
}
if(nodeDis.get(edge.to) > edge.weigth + dis){
nodeDis.put(edge.to,edge.weight + dis);
}
}
set.add(minNode);
minNode = selectMinNode(nodeDis,set);
}
return nodeDis;
}
private static Node selectMinNode(HashMap<Node,Integer> map,Set<Node> set){
int minDis = Integer.MAX_VALUE;
Node minNode = null;
for(Node node : map.keySet()){
if(!set.contains(node) && minDis > map.get(node)){
minNode = node;
minDis = map.get(node);
}
}
return minNode;
}
加强堆
public static class Record{
private Node node;
private Integer dis;
public Record(Node node , Integer dis){
this.node = node;
this.dis = dis;
}
}
public static class NodeHeap{
private Node[] heap;
private HashMap<Node,Integer> indexMap;
private HashMap<Node,Integer> distanceMap;
private int size;
public NodeHeap(Int size){
heap = new Node[size];
indexMap = new HashMap<>();
distanceMap = nee HashMap<>();
}
private void swap(int index1,int index2){
indexMap.put(heap[index1],index2);
indexMap.put(heap[index2],index1);
Node tmp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = tmp;
}
private void heapInsert(int index){
while(distanceMap.get(index-1) /2)>distaceMap.get(index)){
swap((index -1)/2,index);
index = (index - 1)/2;
}
}
private void heapify(int index,int size){
int left = index * 2 + 1;
while(left < size){
int small = left + 1 < size && distanceMap.get(heap[left + 1]) < distanceMap.get(heap[left]) ?
left + 1 : left;
smapp = distanceMap.get(heap[small]) < distanceMap.get(heap[index]) ? small : index;
if(small == index){
break;
}
swap(small,index);
index = small;
left = index * 2 + 1;
}
}
private boolean isEntered(Node node){
return indexMap.containsKey(node);
}
private boolean inHeap(Node node){
return isEbtered(node) && indexMap.get(node) != -1;
}
public void addOrUpdateOrIgnore(Node node,int distance){
if(inHeap(node)){
distanceMap.put(node,Math.min(distanceMap.get(node),distance));
heapInsert(indexMap.get(node));
}
if(!isEntered(node)){
heap[size] = node;
indexMap.put(node,size);
distanceMap.put(node,distance);
heapInsert(size++);
}
}
public Record pop(){
Record record = new Record(heap[0],distanceMap.get(heap[0]));
swap(0,size -1);
indexMap.put(heap[size-1],-1);
distanceMap.remove(heap[size -1]);
heap[size - 1] = null;
heapify(0 , --size);
return record;
}
public boolean isEmpty(){
return size == 0;
}
}
public static HashMap<Node,Integer> dijstra2(Node head,int size){
NodeHeap heap = new NodeHeap(size);
heap.addOrUpdateOrIgnore(head, 0);
HashMap<Node, Integer> ans = new HashMap<>();
while (!heap.isEmpty()){
Record record = heap.pop();
Node cur = record.node;
int dis = record.dis;
for (Edge edge : cur.edges) {
heap.addOrUpdateOrIgnore(edge.to,edge.weight+dis);
}
ans.put(cur,dis);
}
return ans;
}
题目
1.拓扑排序
// 给定一个有向图,图节点的拓扑排序定义如下:
//
// 对于图中的每一条有向边 A -> B , 在拓扑排序中A一定在B之前.
// 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
// 针对给定的有向图找到任意一种拓扑排序的顺序.
// 你可以假设图中至少存在一种拓扑排序
//
// 图结点的个数 <= 5000
// 样例
// 样例 1:
//
// 输入:
// graph = {0,1,2,3#1,4#2,4,5#3,4,5#4#5}
// 输出:
// [0, 1, 2, 3, 4, 5]
//
// 拓扑排序可以为:
// [0, 1, 2, 3, 4, 5]
// [0, 2, 3, 1, 5, 4]
// ...
// 您只需要返回给定图的任何一种拓扑顺序。
//https://www.lintcode.com/problem/127/
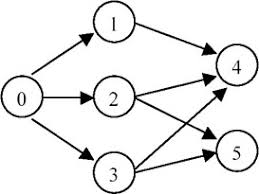
图结构
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
BFS思路
-
弄一个hashMap-indegreeMap,用来记录每个节点的初始入度
-
通过两次for循环,第一次for循环添加每个节点
-
第二次for循环通过node的neightbors,得出每个节点的入度
-
-
弄一个队列queue,和List-ans,队列每次加入入度为0的节点
-
队列弹出的节点加入ans中,然后对节点的neight遍历,减少入度值
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph){
Map<DirectedGraphNode,Integer> indegreeMap = new HashMap<>();
for(DirectedGraphNode node : graph){
indegreeMap.put(node,0);
}
for(DirectedGraphNode node : graph){
for(DirectedGraphNode node : node.neighbors){
indegreeMap.put(node,indegreeMap.get(node)+1);
}
}
Queue<Node> queue = new LinkedList<>();
ArrayList<DirectedGraphNode> ans = new ArrayList<>();
for(DirectedGraphNode cur:indegreeMap.keySet()){
if(indegreeMap.get(cur) == 0){
queue.add(cur);
}
}
while(!queue.isEmpty()){
DirectedGraphNode cur = queue.poll();
ans.add(cur);
for(DirectedGraphNode next : cur.neighbors){
indegreeMap.put(next, indegreeMap.get(next) - 1);
if(indegreeMap.get(next) == 0){
queue.add(next);
}
}
}
return ans;
}
DFS思路
-
节点深度
-
通过最大深度可以确定拓扑排序
-
首先通过递归方程求出每个节点的最大深度,然后根据最大深度进行排序(由大到小,将结果返回)
-
-
点次:这个节点往后经过的节点总数(包括自己)
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph){
HashMap<DirectedGraphNode,Record> map = new HashMap<>();
for(DirectedGraphNode cur : graph){
f(map,cur);
}
ArrayList<Record> list = new ArrayList<>();
for(Record rec : map.values()){
list.add(rec);
}
list.sort(new Comparator<Record>(){
@Override
public int compare(Record o1, Record o2) {
return o1.deep == o2.deep ? 0 : o1.deep > o2.deep ? -1 : 1;
}
});
ArrayList<DirectedGraphNode> ans = new ArrayList<>();
for(Record cur : list){
ans.add(cur.node);
}
return ans;
}
public static class Record{
public DirectedGraphNode node;
public int deep;
public Record(DirectedGraphNode node,int val){
this.node = node;
this.val = val;
}
}
public static int f(HashMap<DirectedGraphNode,Record> map,DirectedGraphNode node){
if(map.containKey(node)){
return map.get(node).deep;
}
int deep = 0;
for(DirectedGraphNode next : node.neighbors){
deep = Math.max(f(map,next),deep);
//点次,就是所有的子节点相加
//deep += f(map,next).deep
}
deep =deep + 1;
map.put(node,new Record(node,deep));
return deep;
}
2.网络延迟时间
// 有 n 个网络节点,标记为 1 到 n。
//
// 给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
//
// 现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
//
//
//
// 示例 1:
//
//
//
// 输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
// 输出:2
// 示例 2:
//
// 输入:times = [[1,2,1]], n = 2, k = 1
// 输出:1
// 示例 3:
//
// 输入:times = [[1,2,1]], n = 2, k = 2
// 输出:-1
//https://leetcode.cn/problems/network-delay-time/
思路:
- 转换为熟悉的图结构,求解每个节点的最近距离,然后从里面挑选最远的一个
public static int networkDelayTime1(int[][] times, int n, int k) {
Graph graph = create(times);
Node from = graph.nodes.get(k);
HashMap<Node, Integer> nodeDis = new HashMap<>();
boolean[] visited = new boolean[n];
nodeDis.put(from, 0);
visited[k - 1] = true;
Set<Node> set = new HashSet<>();
Node minNode = selectMinNode(nodeDis, set);
while (minNode != null) {
int dis = nodeDis.get(minNode);
for (Edge edge : minNode.edges) {
if (!nodeDis.containsKey(edge.to)) {
nodeDis.put(edge.to, edge.weight + dis);
}
if (nodeDis.get(edge.to) > edge.weight + dis) {
nodeDis.put(edge.to, edge.weight + dis);
}
}
set.add(minNode);
visited[minNode.value - 1] = true;
minNode = selectMinNode(nodeDis, set);
}
for (int i = 0; i < n; i++) {
if (!visited[i]) {
return -1;
}
}
int ans = Integer.MIN_VALUE;
for (Integer num : nodeDis.values()) {
ans = Integer.max(ans, num);
}
return ans;
}
private static Node selectMinNode(HashMap<Node, Integer> map, Set<Node> set) {
int minDis = Integer.MAX_VALUE;
Node minNode = null;
for (Node node : map.keySet()) {
if (!set.contains(node) && minDis > map.get(node)) {
minNode = node;
minDis = map.get(node);
}
}
return minNode;
}
public static Graph create(int[][] times) {
Graph graph = new Graph();
for (int i = 0; i < times.length; i++) {
int fi = times[i][0];
int ti = times[i][1];
int wi = times[i][2];
if (!graph.nodes.containsKey(fi)) {
Node from = new Node(fi);
graph.nodes.put(fi, from);
}
if (!graph.nodes.containsKey(ti)) {
Node to = new Node(ti);
graph.nodes.put(ti, to);
}
Node from = graph.nodes.get(fi);
Node to = graph.nodes.get(ti);
Edge edge = new Edge(from, to, wi);
from.nodes.add(to);
from.edges.add(edge);
graph.edges.add(edge);
}
return graph;
}
public static class Graph {
public HashMap<Integer, Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
public static class Node {
private int value;
private ArrayList<Node> nodes;
private ArrayList<Edge> edges;
public Node(int v) {
this.value = v;
this.nodes = new ArrayList<>();
this.edges = new ArrayList<>();
}
}
public static class Edge {
public Node from;
public Node to;
public int weight;
public Edge(Node n1, Node n2, int w) {
from = n1;
to = n2;
weight = w;
}
}
思路:
- 用ArrayList存储每个节点对应的距离,
- 堆存储哪个节点,该节点的距离,这个数组是一维数组,a[0]表示节点,a[1]表示距离
- 和上面思路类似,用boolean[]数组表示访问过的节点
- 根据这些,求出最近距离中的最远值
public static int networkDelayTime1(int[][] times, int n, int k) {
ArrayList<ArrayList<int[]>> edge = new ArrayList<>();
for (int i = 0; i <= n; i++) {
edge.add(new ArrayList<>());
}
for (int[] time : times) {
edge.get(time[0]).add(new int[]{time[1], time[2]});
}
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[1] - b[1]);
heap.add(new int[]{k, 0});
boolean[] used = new boolean[n + 1];
int num = 0;
int max = 0;
while (!heap.isEmpty() && num < n) {
int[] record = heap.poll();
int cur = record[0];
int dis = record[1];
if (used[cur]) {
continue;
}
used[cur] = true;
num++;
max = Math.max(max, dis);
for (int[] next : edge.get(cur)) {
heap.add(new int[]{next[0], dis + next[1]});
}
}
return num < n ? -1 : max;
}
加强堆:
public static class Heap{
public boolean[] used;
public int[][] heap;
public int[] hIndex;
public int size;
public Heap(int n){
used = new boolean[n+1];
heap = new int[n+1][2];
hIndex = new int[n+1];
Arrays.fill(hIndex,-1);
size = 0;
}
public void add(int cur, int delay) {
if (used[cur]) {
return;
}
if (hIndex[cur] == -1) {
heap[size][0] = cur;
heap[size][1] = delay;
hIndex[cur] = size;
heapInsert(size++);
} else {
int hi = hIndex[cur];
if (delay <= heap[hi][1]) {
heap[hi][1] = delay;
heapInsert(hi);
}
}
}
public int[] poll() {
int[] ans = heap[0];
swap(0, --size);
heapify(0);
used[ans[0]] = true;
hIndex[ans[0]] = -1;
return ans;
}
public boolean isEmpty() {
return size == 0;
}
private void heapInsert(int i) {
int parent = (i - 1) / 2;
while (heap[i][1] < heap[parent][1]) {
swap(i, parent);
i = parent;
parent = (i - 1) / 2;
}
}
private void heapify(int i) {
int l = (i * 2) + 1;
while (l < size) {
int smallest = l + 1 < size && heap[l + 1][1] < heap[l][1] ? (l + 1) : l;
smallest = heap[smallest][1] < heap[i][1] ? smallest : i;
if (smallest == i) {
break;
}
swap(smallest, i);
i = smallest;
l = (i * 2) + 1;
}
}
private void swap(int i, int j) {
int[] o1 = heap[i];
int[] o2 = heap[j];
int o1hi = hIndex[o1[0]];
int o2hi = hIndex[o2[0]];
heap[i] = o2;
heap[j] = o1;
hIndex[o1[0]] = o2hi;
hIndex[o2[0]] = o1hi;
}
}
public static int networkDelayTime2(int[][] times, int n, int k) {
ArrayList<ArrayList<int[]>> nexts = new ArrayList<>();
for (int i = 0; i <= n; i++) {
nexts.add(new ArrayList<>());
}
for (int[] delay : times) {
nexts.get(delay[0]).add(new int[] { delay[1], delay[2] });
}
Heap heap = new Heap(n);
heap.add(k, 0);
int num = 0;
int max = 0;
while (!heap.isEmpty()) {
int[] record = heap.poll();
int cur = record[0];
int delay = record[1];
num++;
max = Math.max(max, delay);
for (int[] next : nexts.get(cur)) {
heap.add(next[0], delay + next[1]);
}
}
return num < n ? -1 : max;
}